Perhaps you can assist me with some intuition. I'm looking for the number of zeros of
 : = \frac{\mathrm{d}^m}{\mathrm{d}z^m}\left[\left(\frac{P(z)}{Q(z)}\right)^n\right])
, where
)
and
)
are nonconstant polynomials with no common zeros, and
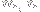
are nonnegative integers. As an example, the case
 = 2(z-1)^4(z-3)(z-7),\:Q(z) = (z+1)(z-2),\:m=0,\:n=5)
yields
 = \frac{32(z-1)^{20}(z-3)^5(z-7)^5}{(z+1)^5(z-2)^5})
, which has thirty zeros (the zeros of the polynomial in the numerator).
For some convenient notation, let
},\: q : = \deg{Q(z)})
and
 = A(z-z_1)(z-z_2)\dots (z-z_q))
, where
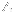
is a complex number. I tried to decompose the rational function
)
in terms of its poles as follows:
 = H_{m,n}(z) + \frac{C_{z_1,1}}{(z-z_1)^{m+1}} + \frac{C_{z_1,2}}{(z-z_1)^{m+2}} + \dots + \frac{C_{z_1,n}}{(z-z_1)^{m+n}} + \frac{C_{z_2,1}}{(z-z_2)^{m+1}} + \frac{C_{z_2,2}}{(z-z_2)^{m+2}} + \dots + \frac{C_{z_q,n}}{(z-z_q)^{m+n}}.\:\: ( 1 ))
Here, the
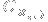
are complex numbers, and
)
is a polynomial of degree
n-m,\,0\})
. Specifically, if
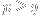
and
n)
(which is precisely when
)
does not vanish), we can write the terms in the right-hand side of equation
)
as a fraction with a common denominator, such that the polynomial
[(z-z_1)(z-z_2)\dots(z-z_q)]^{m+n})
dominates the degree in its numerator. Hence,
)
has
n-m+q(m+n) = pn + (q-1)m)
zeros in this case.
There seem to be two more distinct cases, but I'm not sure how to prove what the number of zeros is in them. The answer in those (remaining) cases should (probably, based on my numerical experiments) be
m)
if
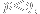
and
-(m+1),)
if
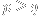
and
n.)
Any ideas?
"Stephen Wolfram is the creator of Mathematica and is widely regarded as the most important innovator in scientific and technical computing today." - Stephen Wolfram


 Similar Threads
Similar Threads
