I fucking suck at math, but I love it. I genuinely wish I had the time to understand it as profoundly as you.
Edit: I'm very curious about math and fuck with numbers in my free time but its not nearly as complex as what you post. A year or so ago I found something cool, I can't remember exactly how/what I was doing but the result would look like something similar: 0.845749350254069765210543.... (infinitely)
So at first glance it just looks like a huge fucking decimal but if you count the numbers between the zeros, they are the same as the number that immediately proceeds the zero (including the first 0 before the decimal point)
0.845749350
I wish I could remember what I was doing, I have it in a notebook somewhere but since I've moved who knows where that's at
|
What you're talking about is basically a repeating decimal. For instance
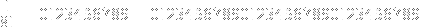
Another interesting example of a repeated fraction is

. It has the additionaly property of it being cyclic. So 2/7 is the same as 1/7 except you move the 14 to the end and start with 2:
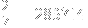
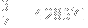
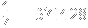
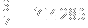
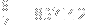
As you can see, not only are they all repeating decimals, but they are all cyclic permutations of the original 1/7 string.
This kind of thing is related to cyclic numbers. These are numbers where successive multiples of that number are also cyclic permutations of that number. The smallest such number in decimal is the same string of numbers as 1/7: 142,857, since 142,857 * 2 = 285,714, etc (same as what is shown above).
Cyclic numbers are always of the form
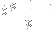
where b is the base you're working in (10 in our case) and p is a prime that does not divide b. Not all primes satisfying this formula will produce a cyclic number, but all cyclic number will satisfy this formula. According to wikipedia, the following are the first to primes produce cyclic numbers:
7, 17, 19, 23, 29, 47, 59, 61, 97, 109, 113, 131, 149, 167, 179, 181, 193, 223, 229, 233, 257, 263, 269, 313, 337, 367, 379, 383, 389, 419, 433, 461, 487, 491, 499, 503, 509, 541, 571, 577, 593, 619, 647, 659, 701, 709, 727, 743, 811, 821, 823, 857, 863, 887, 937, 941, 953, 971, 977, 983
142,857 have b = 10 and p = 7.
The next lowest cyclic number has b = 10 and p = 17: 0,588,235,294,117,647
You have to allow for leading zeros, otherwise 142857 is the only number that is cyclic.
I found those to be a cool math facts, so I thought I would share.


 Similar Threads
Similar Threads
