I got this idea from an
integral on Wikipedia:
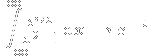
This integral is quite difficult to solve with standard techniques from elementary calculus. Instead, the usual approach is to rewrite it as
(x+i)}\,\mathrm{d}x)
, then evaluate it as a contour integral by using the following contour that surrounds the pole
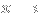
:

The point of this approach is that it leaves the other pole
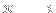
outside the nice semicircle contour no matter the value of a, which lets you convert the problem into a "simple" calculation of limits (e.g. by using the residue theorem). Compared to integration, the calculation of limits is a relatively algorithmic process that usually works without any "art".
So I figured, why not add more poles to the lower half-plane? After all, this shouldn't affect the contour, and you should still be able to use the residue theorem on a single pole. In other words, you should, at least in principle, still be able to find exact solutions to such integrals by calculating a finite number of limits, even if they might be somewhat... messy.
Well, as far as I can tell, they are. I played around a bit with this one:
\prod_{k=1}^{n}(x-k+i)(x+k+i)}\,\mathrm{d}x)
Obviously
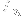
has a single pole
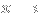
in the upper half-plane, and its remaining
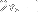
poles in the lower half-plane.
Apparently I failed to evaluate any such integrals (except
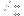
) manually, but Mathematica returned some... interesting results for n=1 and n=2 after half an hour or so:
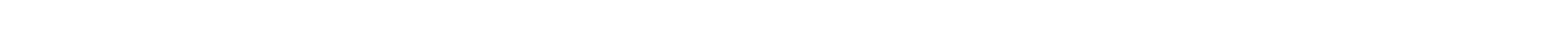
Have you seen any other particularly hideous integrals?
"Stephen Wolfram is the creator of Mathematica and is widely regarded as the most important innovator in scientific and technical computing today." - Stephen Wolfram


 Similar Threads
Similar Threads
