I played around a bit with the word-counting approach, which seems to have given me some promising results.
Each walk of length
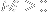
in
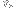
dimensions that starts at the origin corresponds to a word of length
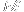
from the alphabet
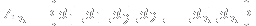
.
For instance, if you're interested in walks from
)
to
)
in
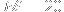
steps, consider the word
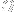
, where

.
The
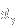
and
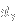
characters correspond to steps in the positive and negative directions in dimension
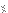
, respectively. The
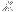
:es are characters (directions) yet to be selected from
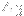
. If we walk in the order prescribed from left to right in
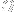
, by the time we reach the
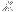
:es, we will have reached
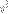
in our walk.
If we consider the first two
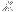
:es from the left, we can replace them with any pair of
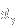
and
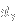
(for fixed
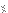
) and still be in
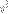
after these two additional steps. Repeating this for each consecutive pair of
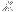
:es, assuming that we have an even number of
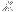
:es, the resulting string describes a walk from the origin to
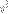
in
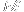
steps.
In this particular example, it is realized that we can represent a selection of three pairs of
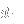
and
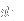
as the sum 3+0+0 (three pairs from the first dimension, none from the remaining two). Similarly, 0+2+1 represents a selection of no pairs of
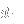
and
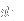
, two pairs of
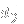
and
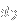
, and one pair of
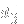
and
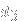
(thus 0+2+1 gives rise to the string
.)
Each such sum with three summands (where the summands are nonnegative integers that sum to half the number of
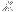
:es) gives us a walk to
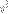
represented by distinct letters.
By counting the number of permutations of all words that arise from all such sums (3+0+0, 0+3+0, 0+0+3, 2+0+1, 2+1+0, 0+2+1, 1+2+0, 0+1+2, 1+0+2, 1+1+1), we get the total number of walks we seek (since no other walks of this type exist).
For this example, we get that the number of walks that we seek, N, is
(Number of walks arising from 3+0+0) + (Number of walks arising from 0+3+0) + ... + (Number of walks arising from 1+1+1) =
!\cdot(0+3)!\cdot3!\cdot0!\cdot0! \cdot 4!} \,+\, \frac{20!}{7!\cdot0!\cdot(3+3)!\cdot(0+3)!\cdot0! \cdot 4!} \,+\, \dots \,+\, \frac{20!}{(7+1)!\cdot(0+1)!\cdot(3+1)!\cdot(0+1)! \cdot(0+1)! \cdot (4+1)!}.)
Dividing N by the total number of walks in 20 steps (
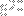
) yields the probability that we end up in
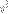
after 20 steps.
This example is easily extended to the general case. For instance, using the notation
,\\ [u]^- = -\min(0,u),)
we get that the probability that we end up in
)
after
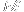
steps is given by
^M}\cdot\sum\frac{1}{\prod_{k=1}^{n} ([x_k]^+ + i_k)! ([x_k]^- + i_k)!})
where the sum is taken over all nonnegative integers
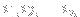
such that
}{2}.)
"Stephen Wolfram is the creator of Mathematica and is widely regarded as the most important innovator in scientific and technical computing today." - Stephen Wolfram