I fucking suck at math, but I love it. I genuinely wish I had the time to understand it as profoundly as you.
Edit: I'm very curious about math and fuck with numbers in my free time but its not nearly as complex as what you post. A year or so ago I found something cool, I can't remember exactly how/what I was doing but the result would look like something similar: 0.845749350254069765210543.... (infinitely)
|
Well, to quote
some guy who broke the "known for" list in the sidebar of Wikipedia by making it too long, "young man, in mathematics you don't understand things. You just get used to them."
As for that number you referred to, MJ already mentioned that it's a repeating decimal, but I might as well write the (elementary) way to convert them into a fraction, since the educational system seems to miss stuff like that sometimes. Let's say that
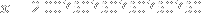
Here, the repeating part is obviously the string 075. We multiply both sides of the equation above by powers of 10 so we first get the repeating part directly after the ., and then so that we also get one string on the left side of the . as follows:
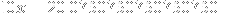
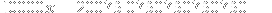
Now note that
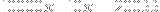
, or equivalently,
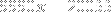
, and thus,
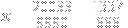
Minor quibble, but shouldn't }(x)) have a g(n) factor in each term? I haven't looked at this with pen and paper, so I might be missing some simplification, but that derivative formula looks wrong at first glance in the general case. have a g(n) factor in each term? I haven't looked at this with pen and paper, so I might be missing some simplification, but that derivative formula looks wrong at first glance in the general case.
|
Well,
}(x) = \sum_{n=0}^{\infty} \frac{g(n)\cdot x^{g(n)-1}}{(g(n))!} = \sum_{n=0}^{\infty} \frac{x^{g(n)-1}}{(g(n)-1)!} = f_{g(n)-1}(x),)
so I think it's fine, and I think it generalizes to replacement of the factorial with the gamma function as well, although I haven't considered the technical details of that carefully.
|
So are you essentially looking for series where such replacements produce things in terms of known special functions? Or am I misunderstanding?
|
Yes, the more elegant the better, in some sense, but you seem to be on the same track in your latest post, so this was probably a superfluous justification. I was inspired by
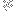
showing up in the closed form of
)
(which isn't really a huge surprise since
/2)
), and by the curious average of the cosine and hyperbolic cosine functions in
.)
Also, the series converges in many cases (e.g. when
)
belongs to a large class of nonconstant and nonlinear polynomials), so I thought it might be interesting to try to find closed forms for some of those cases, since the series hasn't previously been studied in any generality, AFAIK.
}(x) = -\sum_{n=1}^{\infty} \frac{x^{g(n)}}{(g(n))}) has some interesting ones. has some interesting ones.
|
I like that function! The
)
series can be explained with the well-known closed forms of the series
 = \frac{1}{2}\cdot\log{(1-x^2)})
and
 = x-\mathrm{arctanh}\,x)
that you already mentioned (it should be the hyperbolic arctangent, not the regular one), in addition to a shift of the index of summation to deal with the
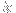
term.
Explicitly, for
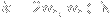
(i.e. when
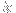
is even),
 = -\sum_{n=1}^\infty \frac{x^{2(n+m)}}{2(n+m)} = -\sum_{n=m+1}^\infty \frac{x^{2n}}{2n} = -\sum_{n=1}^\infty \frac{x^{2n}}{2n} + \sum_{n=1}^m \frac{x^{2n}}{2n} = f_{2n}(x) + \sum_{n=1}^m \frac{x^{2n}}{2n}.)
Similarly, for
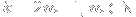
(i.e. when
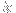
is odd),
 = f_{2n+1}(x) + \sum_{n=1}^m \frac{x^{2n+1}}{2n+1}.)
Note that the larger the value of
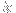
(and thus, of
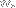
), the better the last sums approximate
)
and
)
, respectively. I haven't investigated it yet, but intuition tells me that
)
and
)
are thus "basis vectors" (in lack of a better term) for the "space" spanned by
,\,k=1,2,3,\dots)
. Perhaps you get some similar "space" with three basis vectors for
)
(which hints at the basis vectors being particularly well-behaved), but again, I haven't explored the idea yet.
To go off on another tangent, if we look at the relation
}(x) = f_{g(n)-1}(x))
from my original series and assume that it holds for your series, it's implied that the "derivative" of
 = x-\mathrm{arctanh}\,x)
is
 = \frac{1}{2}\cdot\log{(1-x^2)})
. Obviously this isn't the standard derivative, but
 = x^2/(x^2-1))
and
 = x/(x^2-1))
are both pretty similar expressions, so I'm thinking there's some type of differential operator
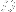
(perhaps it could conveniently be called an "exponential derivative") such that
}(x)) = f_{g(n)-1}(x))
for your series, which might have some very interesting properties.
For the example above,
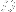
seems to be the operation "differentiate, divide by x, integrate" (with some minor technical tweaks), but it's probably more complicated than that in general...
"Stephen Wolfram is the creator of Mathematica and is widely regarded as the most important innovator in scientific and technical computing today." - Stephen Wolfram