| |
|
|
|
 |
 Posted 2018-12-06, 09:49 AM
in reply to Chruser's post starting "Well, to quote some..."
Posted 2018-12-06, 09:49 AM
in reply to Chruser's post starting "Well, to quote some..."
|
 |
 |
 |
For the example above, 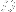 seems to be the operation "differentiate, divide by x, integrate" (with some minor technical tweaks), but it's probably more complicated than that in general... seems to be the operation "differentiate, divide by x, integrate" (with some minor technical tweaks), but it's probably more complicated than that in general...
|
Actually, this seems to be it (modulo some minor technical stuff). My previous post was getting a bit lengthy, so I'll post some calculations in here instead.
We have that
}(x) = -\sum_{n=1}^\infty\frac{x^{g(n)}}{g(n)},)
so
}(x)}{x} = -\sum_{n=1}^\infty x^{g(n)-2}.)
Consequently, by integrating both sides of the equation above and dropping the constant of integration, and by assuming that the order of integration and summation is interchangeable, we see that
}(x)}{x}\,\mathrm{d}x = -\sum_{n=1}^\infty \int x^{g(n)-2}\,\mathrm{d}x = -\sum_{n=1}^\infty\frac{x^{g(n)-1}}{g(n)-1} = f_{g(n)-1}(x).)
In other words, a differential operator 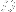 (in the fractional calculus sense, where integration is considered differentiation of order -1) such that }(x)) = f_{g(n)-1}(x)) is
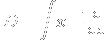
I can't say that I've seen it previously, but I like its symmetry...
"Stephen Wolfram is the creator of Mathematica and is widely regarded as the most important innovator in scientific and technical computing today." - Stephen Wolfram
Last edited by Chruser; 2018-12-10 at 11:32 AM.
|
 |
 |
 |
|
|

|
|
|
|
|
|