| |
|
|
|
 |
 Posted 2018-12-03, 09:25 PM
in reply to Chruser's post "Maclaurin series similar to those of e^x"
Posted 2018-12-03, 09:25 PM
in reply to Chruser's post "Maclaurin series similar to those of e^x"
|
 |
 |
 |
I was playing around with functions of the form }(x) = \sum_{n=0}^{\infty} \frac{x^{g(n)}}{(g(n))!}) (based on the trivial Maclaurin expansion of (based on the trivial Maclaurin expansion of ) ), and noticed, for example, that ), and noticed, for example, that
=\cosh(x),)
=\sinh(x),)
=\cosh(x)-1,)
=\sinh(x)-x,)
=\frac{\cosh(x) + \cos(x)}{2},)
=\frac{\sinh(x) + \sin(x)}{2},)
=\frac{\cosh(x) - \cos(x)}{2},)
=\frac{\sinh(x) - \sin(x)}{2},)
=\frac{e^x}{5} + \frac{2}{5}\left(e^{-\varphi x/2}\cos\left(\frac{1}{2}\sqrt{\sqrt{5}\varphi^{-1}}x\right)+e^{\varphi^{-1}x/2} \cos\left(\frac{1}{2}\sqrt{\sqrt{5}\varphi}x\right )\right),)
where 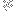 is the golden ratio. If you're sufficiently bored, you should help me find other, interesting functions is the golden ratio. If you're sufficiently bored, you should help me find other, interesting functions ) , or similar series expansions, e.g. by using WolframAlpha. I suspect that the series above have been studied in some more general context since they're so "obvious", but I haven't seen anything along those lines previously. , or similar series expansions, e.g. by using WolframAlpha. I suspect that the series above have been studied in some more general context since they're so "obvious", but I haven't seen anything along those lines previously.
(Edit: I should note that }(x) = f_{g(n)-1}(x)) if you throw away any terms such that if you throw away any terms such that  = 0) .) .)
|
Minor quibble, but shouldn't }(x)) have a g(n) factor in each term? I haven't looked at this with pen and paper, so I might be missing some simplification, but that derivative formula looks wrong at first glance in the general case.
I'm also not sure I understand what you're looking for. Sin, sinh, etc are all essentially special functions, and you could always define special functions based on whatever series you come up with by replacing n with 2n or what have you. So are you essentially looking for series where such replacements produce things in terms of known special functions? Or am I misunderstanding?
Last edited by Demosthenes; 2018-12-03 at 09:49 PM.
|
 |
 |
 |
|
|

|
|
|
|
|
|